Oskar Barnack (1879-1936)
Oskar Barnack and the 3:2 Aspect Ratio
The origin of the aspect ratio of 35mm film can be traced to Oskar Barnack, an employee of Leitz Camera (Leica) in Germany. At the turn of the century, film for still photography came in the form of large plates, which were required in order to make contact prints of the same size (usually 8×10 inches). Driven by a vision of “small negatives–large images”, Barnack revolutionized photography by eliminating the need for large photographic plates and the clumsy camera bodies they required. He demonstrated that high quality prints could be achieved by enlarging images from small negatives exposed on the same 35mm gauge film used in cinema. He created the standard 35mm still frame (24x36mm) simply by merging two 35mm cinema frames (18x24mm). This resulted in a 3:2 aspect ratio compared to the standard 4:3 aspect ratio of early cinema. Barnack then created the first 35mm camera ever, dubbed the “Ur-Leica”, in 1914. After WWI, Barnack convinced his boss, Ernest Leitz II, to begin production of 35mm cameras. In 1925, Leitz Camera released the first Leica and the rest is history.

How has the 3:2 aspect ratio of 35mm film lasted for nearly 100 years as the dominant ratio in still photography? There are many other popular formats in still photography, including 8×10, 4×5, 6×6, and recently 4×3, but there is something special about the 3:2 aspect ratio of 35mm film which has allowed it to endure, and I believe it has nothing to do with how easy it is to find frames for or the availability of correctly sized paper stock for prints or how flexible the format is for cropping, advantages often associated with other aspect ratios. The 3:2 aspect ratio has every logical reason going against it, except that it happens to have the closest proportions to the Golden Rectangle of any other major film format in still photography which, I contend, gives it the potential to present the most aesthetically pleasing composition of all major film formats.
Figure 1: Comparison of various film formats

What Is the Golden Rectangle?
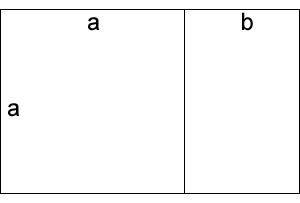
The Golden Rectangle is defined as a rectangle that can be partioned into a square and a smaller rectangle which has the same aspect ratio of the original rectangle. In Figure 2, we see such a rectangle. In this example, the length of the smaller rectangle divided by its width is equal to the length of the larger rectangle divided by its width, i.e., a ÷ b = (a + b) ÷ a. The ratio of the larger side of each rectangle to the smaller side is known as the Golden Ratio. Mathematically, this works out to be about 1.62:1, or 3.2:2 compared to the 3:2 aspect ratio of 35mm film.
Figure 2: The Golden Rectangle
The Golden Rectangle in Nature
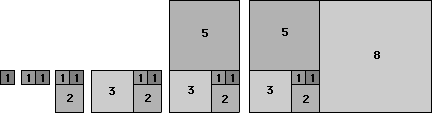
The Golden Rectangle and Golden Ratio appear in some very interesting places. For example, in Fibonacci numbers, a sequence of numbers where each new number is the sum of the previous two numbers (1, 1, 2, 3, 5, 8, 13 . . .), the ratio of consecutive numbers increasingly approaches the Golden Ratio. In Figure 3, we see a graphical relationship between Fibonacci numbers and the Golden Rectangle. The Fibonacci numbers are closely related to exponential growth, such as the reproduction of rabbits. They are also found in plants where many tend to have a Fibonacci number of petals or leaves.
Figure 3: Relationship between the Fibonacci sequence and the Golden Rectangle
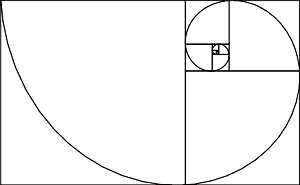
Another interesting place the Golden Rectangle appears is in spirals. Successive points dividing a golden rectangle into squares lie on a logarithmic spiral, also known as the “Spira Mirabilis”. See Figure 4. Coincidentally, spirals such as these are found throughout nature, such as in the contours of Nautilus shells.
Figure 4: The Golden Rectangle and Spira Mirabilis
The Golden Rectangle in Art
The Golden Rectangle is believed to have been first constructed by Pythagorus in the 6th Century B.C. It is said to be one of the most visually pleasing of all geometric forms. Archeologists have found countless examples of it in the facades of ancient Greek architecture. In Figure 5, we see how the Parthenon in Athens was built to the dimensions of the Golden Rectangle.
Figure 5: The Parthenon

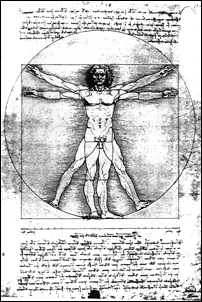
In Figure 6, we also see how Leonardo da Vinci applied the Golden Rectangle to the proportions of the human body. In this example, the height of the person was divided into two segments, the dividing point being the person’s navel. Leonardo took the distance from the soles of the feet to the navel, then divided by the distance from the navel to the top of the head and found that it was equal to the Golden Mean, or as he would call it, the Divine Proportion.
Figure 6: Leonardo da Vinci’s study of the human body